Question

For the graph shown, select the statement that best represents the given system of equations 5y-2x=5 2y+x = -4

consistent and independent
inconsistent
coincident
not enough information

Answer 1

Consistent and Independent.

Explanation:

The given systems of equations is

`\left \{ {{5y-2x=5} \atop {2y+x=-4}} \right.`

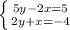
To solve this system, we can multiply the second equation by two, then we sum then

`\left \{ {{5y-2x=5} \atop {4y+2x=-8}} \right.`

`9y=-3\\y=-(3)/(9)\\ y=-(1)/(3)`

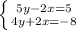
Then, we find the other value replacing this one.

`5(-(1)/(3))-2x=5\\ -(5)/(3)-2x=5\\ -2x=5+(5)/(3)\\ x=(15+5)/(3) / -2\\ x=(20)/(3) * -(1)/(2)\\ x=-(10)/(3)`

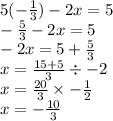
The image attached show the system graphed, where the solution is (-10/3, -1/3).

As you can observe in the image, or in our calculations, the given system is consistent because it has at least one solution. However, this system is also independent, because it has only one solution.

Therefore, the answer is "consistent and independent".

Answer 2

By graphing the given system of equations ( see the attached figure )

5y - 2x = 5

2y + x = -4
As shown in the graph, the lines are intersected in the point ( -10/3 , -1/3 )

So, the correct answer will be ⇒⇒⇒ consistent