Question

A fair, twenty-faced die has $19$ of its faces numbered from $1$ through $19$ and has one blank face. another fair, twenty-faced die has $19$ of its faces numbered from $1$ through $8$ and $10$ through $20$ and has one blank face. when the two dice are rolled, what is the probability that the sum of the two numbers facing up will be $24?$ express your answer as a common fraction.

Answer 1

Represent 24 as a sum of two numbers, first number from first die and second number from second die.
24=19+5=18+6=17+7=16+8=14+10=13+11=12+12=11+13=10+14=9+15=8+16=7+17=6+18=5+19=4+20 (the sums 15+9 and 20+4 are absent, because there aren't numbers: 20 on the first die and number 9 on the second die). Totally, you receive 15 different representations of 24.
The probability that the sum of the two numbers facing up will be 24 is


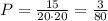`P= (15)/(20\cdot 20) = (3)/(80)` (here
`20\cdot 20` means that you have 20 possibilities to roll first number or blank face on the first die and 20 possibilities to roll number or blank face on the second die).