Question

Let $abcdefgh$ be a cube of side length 5, as shown. let $p$ and $q$ be points on $\overline{ab}$ and $\overline{ae}$, respectively, such that $ap = 2$ and $aq = 1$. the plane through $c$, $p$, and $q$ intersects $\overline{dh}$ at $r$. find $dr$.

Answer 1

Let's buils the intersection plane:
Point P is on AB and AP=2, then PB=3; point Q is on AE and AQ=1, then QE=4. Let P' be a point on CD such that CP'=2 and Q' be a point on the plane CDHG such that P'Q'=1 and P'Q' is perpendicular to CD. The line CQ' intersects HD at point R and the plane CPQR is intersection plane.
Consider triangles ΔCDR and ΔCP'Q', they are similar. So,

`(CP')/(CD)= (P'Q')/(RD) \\ (2)/(5) =(1)/(RD) \\ RD=2.5`,
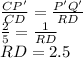
so R is a midlepoint of the side HD (for details see picture).