Question

How much would $500 invested at 6% interest compounded monthly be worth after 5 years? Round your answer to the nearest cent. A(t)=P(1+r/n)^nt

Answer 1

$674.42.

Explanation:

Givens

• The principal of the investment is $500.
• The interest rate compounded monthly is %6 or 0.06.
• The time invested is 5 years.

To solve these type of problems, we need to recur to Interest Compound Formula, which is

`A(t)=P(1+(r)/(n) )^(nt)`

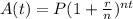
Where
`A` is the total amount of money after the time compounded,
`P` is the principal,
`r` is the interest rate,
`n` is the number of compounded periods in one year and
`r` is time in years.

So,

`P=500\\r=0.06\\n=12\\t=5`

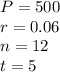
If the problem states that the interest is compounded monthly, then there are gonna be 12 compounded periods in one year. Replacing all these values, we have

`A(t)=P(1+(r)/(n) )^(nt)\\A(t)=500(1+(0.06)/(12) )^(12(5))\\ A(t)=500(1.005)^(60)= 674.42`

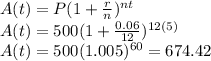
Therefore, the total amount of money after 5 years is $674.42.