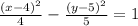Question

Write the equation of the hyperbola with foci at (1, 5) and (7, 5) and with vertices at (2, 5) and (6, 5).

Answer 1

If you plot the points given on a coordinate plane you see that this is a hyperbola that is is horizontal in nature, meaning it opens side to side, not up and down. We can determine the center of it by taking the point equidistant from the vertices, which is (4, 5), the h and k of our center, respectively. Also, the equation looks like this when it is horizontal:
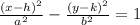
`((x-h) ^(2) )/( a^(2) ) - ((y-k) ^(2) )/( b^(2) ) =1`. a is the distance between the center and the vertices, so our a = 2, and c is the distance between the center and the foci, so our c = 3. We need to find b now, using Pythagorean's theorem.
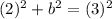
`( 2)^(2) + b^(2) =( 3)^(2)` and
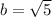
`b= √(5)`. Now we have everything we need to rewrite the equation:
`((x-4) ^(2) )/(4) - ((y-5) ^(2) )/(5) =1`