The formula for compound continuously rate
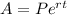
.
Where is A (future amount) = 2519, P (initial amount) = 2300, e is the mathematical constant, r (rate of interest) which is unknown, and t (time in years) = 20
Now we plug in the variables into the equation.
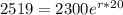
It is asking for the rate, so must isolate

.
First we divide 2300 on both sides of the equation.
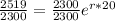

Then we enter the inverse of

, which is log.
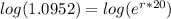
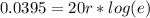
Then divide
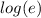
on both sides.
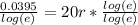
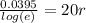
Then divide 20 on both sides.

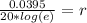
Finally solve for

0 = r
The answer is r = 0%