Question

What is the vertex of the graph of y = 1/3 (x-9)2 + 5 Question 1 options: (9,5) (3,3) (3,5) (-9,5)

Answer 1

`\bf ~~~~~~\textit{parabola vertex form} \\\\ \begin{array}{llll} y=a(x- h)^2+ k\\\\ x=a(y- k)^2+ h \end{array} \qquad\qquad vertex~~(\stackrel{}{ h},\stackrel{}{ k})\\\\ -------------------------------\\\\ y=\cfrac{1}{3}(x-\stackrel{h}{9})^2+\stackrel{k}{5}\qquad \qquad vertex~(9,5)`

Answer 2

ANSWER

The vertex of the graph of

`y = (1)/(3) {(x - 9)}^(2) + 5`
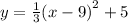
is


`(9,5)`



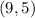
Step-by-step explanation

The vertex form of a parabola is given by


`y = a {(x - h)}^(2) + k`

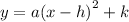
where

`V(h,k)`
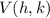
is the vertex of the parabola.


The function given to us is


`y = (1)/(3) {(x - 9)}^(2) + 5`
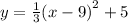
This is already in the vertex form.


When we compare this to the general vertex form, we have,


`a = (1)/(3)`


`h = 9`
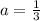
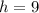
and


`k = 5`


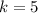
Therefore the vertex of the parabola is


`V(9,5)`

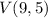
Hence the correct answer is option A.