Answer:
The correct answer is B
Explanation:
Step 1
The first step in identifying the graph of the function is to determine where the vertical asymptotes occur. The vertical asymptotes occurs where the expression in the numerator is zero,
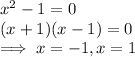 .
.
The next step is to calculate the
 intercept. The
intercept. The
 intercept occurs where
intercept occurs where
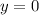 . We determine intercept as shown below,
. We determine intercept as shown below,
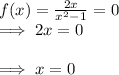
Step 2
The next step is to find the
 intercept. The
intercept. The
 intercept occurs when
intercept occurs when
 . We determine the
. We determine the
 intercept as shown below,
intercept as shown below,
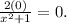
The
 intercept occurs at
intercept occurs at
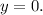
Step 3
We now investigate the behavior of the function for different values of
 . We can tell that
. We can tell that
,

Step 4
The only graph that has vertical asymptotes at
 and that crosses goes through
and that crosses goes through
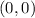 and meets all the conditions in Step 3 is the second graph B.
and meets all the conditions in Step 3 is the second graph B.