Question

Which expression is equivalent to tan^2(a/2)

Answer 1

Without knowing what the possible answer choices are, perhaps this is one of them:


`\tan^2\frac a2=(\sin^2\frac a2)/(\cos^2\frac a2)=\frac{\frac{1-\cos a}2}{\frac{1+\cos a}2}=(1-\cos a)/(1+\cos a)`

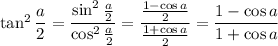
We can rewrite this in several ways, but one that should immediately occur to you is to consider writing the denominator in terms of
`\sin a`:


`(1-\cos a)/(1+\cos a)\cdot(1-\cos a)/(1-\cos a)=(1-2\cos a+\cos^2a)/(1-\cos^2a)=(1-2\cos a+\cos^2a)/(\sin^2a)`

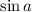
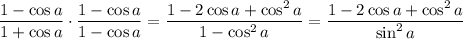
We can further write this in terms of the reciprocal functions,


`\frac1{\sin^2a}-(2\cos a)/(\sin^2a)+(\cos^2a)/(\sin^2a)=\csc^2a-2\csc a\cot a+\cot^2a`

and so on...