You have one of those equations already solved for y, so part of the hard stuff is done, at least. Let's sub that y value in for y in the other equation and simplify, like this:
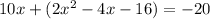
. Combining like terms and setting this equal to 0 so we can solve for x gives us this:

. When you factor that, you will get 2 values for x. They are x = -1 and x = -2. Let's see which one works. When x = -1:
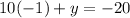
and -10 + y = -20. Therefore, y = -10. Let's see if -10 works in the other equation too when x is -1:
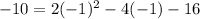
. That simpifies down to -10 = -10, so the solution of (-1, -10) works. Let's see what happens if we try x = -2. Solving for y, we have 10(-2) + y = -20 and we find that y = 0. If we replace 0 in the other equation for y we get:

and that simplifies to 0 = 0. Therefore, both of these solutions work. Let me tell you why. We have a line intersecting a parabola. By the fact that both of the solutions work, that means that the line intersects the parabola in 2 places, which is common in this type of system. 2 lines can only intersect in 1 place, but this is a line and a quadratic.