Question

If a fixed number is added to each term of an arithmetic​ sequence, is the resulting sequence an arithmetic​ sequence?

Answer 1

Yes. But, if the number is multiplied/divided, then it would be a geometrical.

Answer 2

Answer: Yes, the resulting sequence is an arithmetic sequence.

Step-by-step explanation: Given that a fixed number is added to each term of an arithmetic​ sequence.

We are to check whether the resulting sequence is an arithmetic one or not.

Let the first term of an arithmetic sequence is a and its common difference is d.

Then, the first few terms of the sequence are given by

`a,~a+d,~a+2d,~a+3d,~~.~~.~~.`

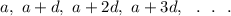
Now, if we add a fixed number k to each term of the sequence, then the sequence will be pf the form :

`a+k,~a+d+k,~a+2d+k,~a+3d+k,~~.~~.~~.`

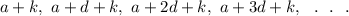
Here, we notice that

first term is (a + k) and

`(a+d+K)-(a+k)=(a+2d+k)-(a+d+k)=(a+3d+k)-(a+2d+k)=~~.~~.~~.~~=d.`

Therefore, the difference between the consecutive terms in the resulting sequence will also be d.

Thus, the resulting sequence is an arithmetic sequence with first term (a + k) and common difference d.

The answer is YES.