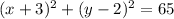The equation for the midpoint is given by:
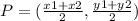
Substituting values we have:
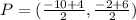
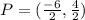
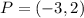
We can find the radius of the circle using the equation of distance between points:
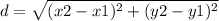
Substituting values:
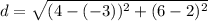
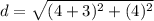
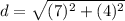
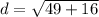
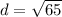
The equation of the circle is its standard form is:
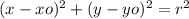
Where,
(xo, yo): coordinates of the center of the circle
r: radius of the circle
Substituting values: