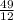Question

For what values of m does the graph of y = 3x2 + 7x + m have two x-intercepts?

Answer 1

Think "discriminant." There will be 2 real roots (x-intercepts) so long as the discriminant is ≥ 0.

Form the discriminant: b^2 - 4ac becomes 7^2 - 4(3)(m).

Write and solve the inequality 49-12m≥0.

Add 12 m to both sides: 49 ≥ 12m
Divide both sides by 12: 49/12 ≥ m

So long as m is 49/12 or smaller, there will be 2 real roots. These roots could be equal, but also could be unequal.

Answer 2

Value of m must be less than
`(49)/(12)`

Explanation:

Given: Equation of curve,
`y=3x^2+7x+m`

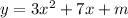
To find: 2 x-intercepts

X-intercept of curve means zeroes of quadratic equation we get by putting y = 0.

So, The quadratic equation we get,

`3x^2+7x+m=0`

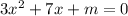
Now, to have 2 x-intercept the discriminant of the quadratic equation should be greater than 0.

Therefore, By using this condition we find value of m for which given equation has 2 x-intercept.

Discriminant, D =
`√(b^2-4ac)`

where, a = coefficient of
`x^2`

b = coefficient of
`x`

c = constant term

⇒ a = 3, b = 7 & c = m

Putting these value and applying the condition of discriminant we get,

D > 0

⇒
`√(7^2-4*3* m)>0`

⇒
`√(49-12* m)>0`

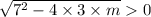
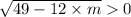
Squaring both sides,

⇒
`49-12* m>0`

⇒
`49>12* m`

⇒
`m<(49)/(12)`

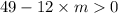
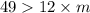
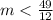
Therefore, Value of m must be less than
`(49)/(12)`