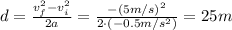Question

Cole is riding a sled with initial speed of 5 m/s from west to east. the frictional force of 50 n exists due west. the mass of the sled and cole together is 100 kg. how far does the sled go before stopping? use the formula: a= (vf2-vi2)/2d regarding the relation among acceleration a, final velocity vf, initial velocity vi and the traveled distance of an object

d.

Answer 1

We can calculate the acceleration of Cole due to friction using Newton's second law of motion:

`F=ma`
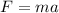
where
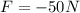
`F=-50 N` is the frictional force (with a negative sign, since the force acts against the direction of motion) and m=100 kg is the mass of Cole and the sled. By rearranging the equation, we find

`a= (F)/(m)= (-50 N)/(100 kg)=-0.5 m/s^2`

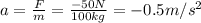
Now we can use the following formula to calculate the distance covered by Cole and the sled before stopping:

`a= (v_f^2-v_i^2)/(2d)`
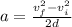
where

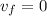
`v_f=0` is the final speed of the sled

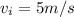
`v_i=5 m/s` is the initial speed

`d` is the distance covered

By rearranging the equation, we find d:

`d= (v_f^2-v_i^2)/(2a)= (-(5 m/s)^2)/(2 \cdot (-0.5 m/s^2))=25 m`