Answer:
Option D is correct.
 and reflected across x = -1
and reflected across x = -1
Explanation:
From the given figure:
The coordinates of ABC are:
A(-7, 2), B(-3, 5) and C(-3, 1)
first apply the rule of translation on ABC i.e:

Then;
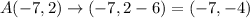

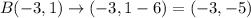
Next, reflect it across x = -1
The rule of reflection across x = -1 i.,e
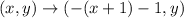
or
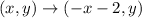
then;
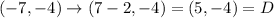
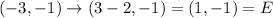
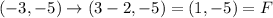
Therefore, the glide reflection describes the mapping ABC to DEF is:
 and reflected across x = -1
and reflected across x = -1