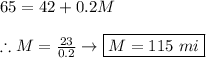This is a problem of
System of Equations. So in this problem we have two rental car companies. Thus, we can write a system of equation by analyzing the statements step by step:
One rental car company charges $65 per day with unlimited miles:
That is the final cost you will pay, in dollars, at the end of the day, by using the car will be:
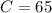
This is true because this company offers you a plan for unlimited miles.
Another rental car company charges $42 per day plus $0.20 per mile:
In a mathematical language that is:
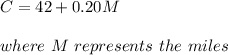
Therefore, for a one-day rental, the mileage that makes the cost of the two options equal is: