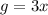Answer:
The answer is
Explanation:
In order to determine the value of "g", we have to know about equations. In any equation, the equality has to fulfill on each side. For example, if we have the next equation: x=2, the "x" must be 2 to fulfill the equality.
In this case, we need a "g" value to fulfill the equality represents by the left side of the equation.
Then:
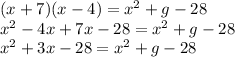
We can see that the value of "g" must be "3x" because we already fulfill the
 and -28.
and -28.
Therefore, the value of "g" is