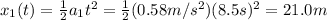a) Both players are moving by uniformly accelerated motion, and we can write the position at time t of each of the two players as follows:
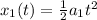
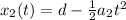
where
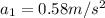
is the acceleration of the first player
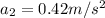
is the acceleration of the second player
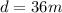
is the initial distance between the two players
and where I put a negative sign in front of the acceleration of the second player, since he's moving in the opposite direction of the first player.
The time t at which the two players collide is the time t at which

, therefore:
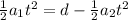
from whic we find

b) We can use the equation of
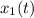
to find how far the first player run in t=8.5 s: