Answer: The required additive inverse of the given polynomial is

Step-by-step explanation: We are given to find the additive inverse of the following polynomial :

Let Q be the polynomial that represents the additive inverse of the polynomial P.
Then, the sum of the polynomials P and must be zero.
That is,
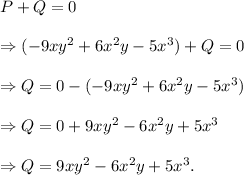
Thus, the required additive inverse of the given polynomial is
