
will be continuous at
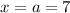
if
(i)
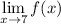
exists,
(ii)
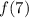
exists, and
(iii)
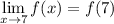
.
The second condition is immediate, since
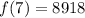
has a finite value. The other two conditions can be established by proving that the limit of the function as
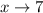
is indeed the value of
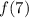
. That is, we must prove that for any
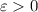
, we can find
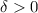
such that
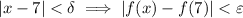
Now,
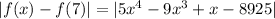
Notice that when
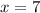
, we have

. By the polynomial remainder theorem, we know that
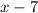
is then a factor of this polynomial. Indeed, we can write
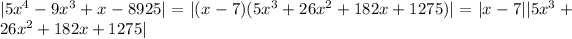
This is the quantity that we do not want exceeding

. Suppose we focus our attention on small values
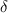
. For instance, say we restrict
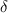
to be no larger than 1, i.e.
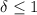
. Under this condition, we have
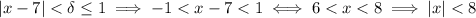
Now, by the triangle inequality,
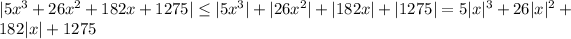
If
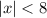
, then this quantity is moreover bounded such that
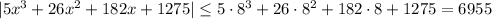
To recap, fixing
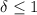
would force
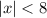
, which makes
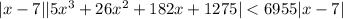
and we want this quantity to be smaller than

, so
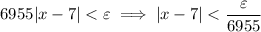
which suggests that we could set
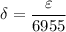
. But if

is given such that the above inequality fails for
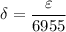
, then we can always fall back on

, for which we know the inequality will hold. Therefore, we should ultimately choose the smaller of the two, i.e. set
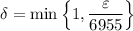
.
You would just need to formalize this proof to complete it, but you have all the groundwork laid out above. At any rate, you would end up proving the limit above, and ultimately establish that

is indeed continuous at
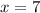
.