Answer:
x=3, 4, or 5
Explanation:
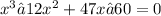
First we have to determine one value of x by hit and trial method for which , the above polynomial becomes 0
on trying random values of x , we sees that for x = 3 , the polynomial becomes 0
Hence (x-3) is one of the factor
Hence now let us move with the factorization part
The above polynomial can be re written as
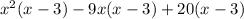
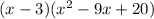
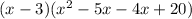
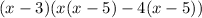

hence we have our
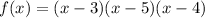
In order to find the zeroes we put f(x) =0
Hence
[tex](x-3)(x-5)(x-4)=0
Therefore
if (x-3)=0 , x=3
if (x-5) , x= 5
if (x-4), x=4