Answer:
interquartile range = 12
Option D is correct option.
Explanation:
We need to determine the interquartile range of the data in the box plot below.
The boxplot is made up of
Minimum Value, First Quartile, Median, Third Quartile and Maximum Value
Looking at the box plot, we get:
Minimum Value: 72
First Quartile: 73
Median: 80
Third Quartile: 85
Maximum Value: 95
The formula used to find interquartile range is:
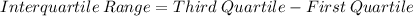
Putting values of First Quartile: 73 and Third Quartile: 85 we can find interquartile range
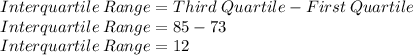
SO, we get interquartile range = 12
Option D is correct option.