Question

one half of a number is added to 9, giving thr result of at least 4. Find the unknown numbers in the description.

Answer 1

Hey there!

We'll call this number x. Using some keywords and prior knowledge, we can translate this English into math.

Our keyword is of. When we say of, it means multiply. Why?

For example, if we wanted 1/2 of 4, we would compute:

1/2 * 4 = 4/2 = 2

And in your head, if we wanted two equal groups of 4, there'd be 2 in each. We say two equal groups because multiplying by 1/2 is the same as dividing by 2.

Therefore, we have 1/2 of a number, giving us:


`(1)/(2)x`

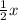
Next, we know we're adding this result to 9.


`(1)/(2) x + 9`

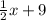
Here's where it can get a bit tricky. We want this value (above) at least four. That means that the value can be equal to four, but it could also be greater. That means our sign is greater than or equal to:


`(1)/(2) x + 9 \geq 4`

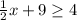
We can then subtract 9 from both sides:


`(1)/(2) x \geq -5`

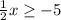
Multiply both sides by 2:


`x \geq -10`

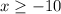
Therefore, x can be -10 or more. Some examples are -10, -9, -8, and so on.

If we try -8:


`(1)/(2)(-8)+9 \geq 4`


`-4+9 \geq 4`


`5 \geq 4`

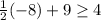
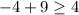
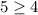
Therefore, we're correct.

Hope this helps!