Please take the time to type in the question by yourself. I assume you use some kind of an apps to transcribe problems. It only confuses and discourages helpers. The fact that the question was reported means it is not clear.
I ASSUME the question is as follows:
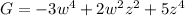
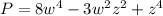
Need to find P-G.
We see clearly that each expression P, G contains 3 terms, namely w^4, w^2z^2 and z^4. We will have to add/subtract like terms to get the answer.
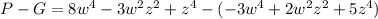
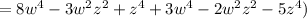
(distribute negative sign into expression G)
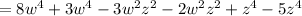
(group like terms)
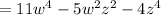
(add/subtract like terms)