Question

How many ordered pairs of positive integers $(x,y)$ satisfy the equation $\frac{x}{y} = \frac{225}{xy} + \frac{y}{x}$?

Answer 1

Let's solve the equation
`(x)/(y) = (225)/(xy) + (y)/(x)`.

`(x)/(y) = (225+y^2)/(xy)`.
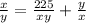
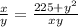
Since x>0, y>0, the equation is
`x= (225+y^2)/(x) \Rightarrow x^2=225+y^2\Rightarrow x^2-y^2=225`.

`(x-y)(x+y)=3\cdot3\cdot5\cdot5`.
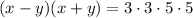
The divisors of 225 are: 1, 3, 5, 9, 15, 25, 45, 75, 225. Notice that x-y<x+y, that's why all positive integer solutions of the equation are solutions of the next systems.

`\left \{ {{x-y=1} \atop {x+y=225}} \right. \rightarrow \left \{ {{x=113} \atop {y=112}} \right.`

`\left \{ {{x-y=3} \atop {x+y=75}} \right. \rightarrow \left \{ {{x=39} \atop {y=36}} \right.`

`\left \{ {{x-y=5} \atop {x+y=45}} \right. \rightarrow \left \{ {{x=25} \atop {y=20}} \right.`

`\left \{ {{x-y=9} \atop {x+y=25}} \right. \rightarrow \left \{ {{x=17} \atop {y=8}} \right.`
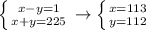
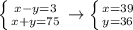
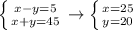
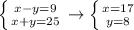
All the rest combinations will provide not positive integer solutions.
Answer: (113,112), (39,36), (25,20), (17,8), (15,0)