Answer:
The correct option is 1. The given statement is true.
Explanation:
The binomial expansion is defined as
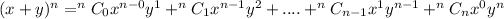
The rth term in a binomial expansion is defined as
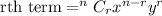
Let the coefficient of
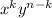 be A. The power of x is k and the power of y is n-k. It means
be A. The power of x is k and the power of y is n-k. It means
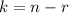

The coefficient of
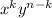 is
is
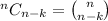
Using the property of combination,
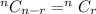
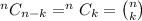
The coefficient of
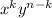 is
is
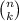 . Therefore the given statement is true.
. Therefore the given statement is true.