Question

Solve the radical equation x – 7 = square root of -4x+28. Which statement is true about the solutions to the radical equation? There are no true solutions. There are two true solutions. There is one extraneous solution, with a value greater than 4. There is one true solution, with a value greater than 6.

Answer 1

B. There are two true solutions

Explanation:

(the two solutions would be x=3 and x=7)

Answer 2

x = 3 and 7

There are two true solutions.

Explanation:

To solve
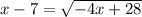`x-7 = √(-4x+28)`, use inverse operations by squaring both sides of the equal sign.

`(x-7)^2 = (√(-4x+28))^2\\x^2-14x+49 = -4x+28\\x^2-14x+4x+49-28 = 0\\x^2-10x+21=0`

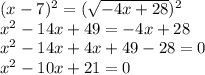
The quadratic expression can be factored into binomials and set equal to 0 by the zero product property to find x.

(x - 3) ( x - 7) = 0

x-3 = 0 so x=3

x-7 = 0 so x=7

Now check each solution into the original equation to be sure it solve the solution and is not extraneous.

`7-7 = √(-4(7)+28)\\ 0=0`

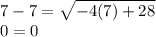
and

`3-7 = √(-4(3)+28)\\[tex]-4 = √(16)\\-4 =-4`[/tex]