To graph each equation, you should first plot the y-intercepts. The y-intercept is 3 for the first equation and 10 for the second [see picture 1].
Next, observe the slope. In the first equation, it's

. Since you write slope in
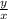
or rise-over-run format, you would rise 1 unit and run 4 units right to get the next point. In a similar way, you could go down 1 unit and run 4 units left to get another point, since
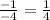
. Fill in as many points on the plane as you can, then connect them with a line [see picture 2].
The slope of the second equation is 2, or
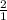
, meaning we would rise 2 and run 1 right. Plot these points and connect then with a line [see picture 3].
After observing the graph, we can see that the intersection point is at (4, 11).