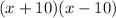Question

Part A: Factor 5x2a2 − 19xa2 − 4a2. Show your work. (4 points) Part B: Factor x2 + 14x + 49. Show your work. (3 points) Part C: Factor x2 − 100. Show your work. (3 points)

Answer 1

Part A:
For this case we have the following polynomial:

`5x ^ 2a ^ 2 - 19xa ^ 2 - 4a ^ 2`
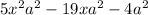
First we make a common factor a^2:
We have then:

`a ^ 2 (5x ^ 2 - 19x - 4)`
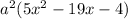
From here, we can factor the quadratic expression into parentheses.
We have then:

`a ^ 2 ((5x + 1) (x-4))`
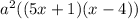Answer:

`a ^ 2 ((5x + 1) (x-4))`

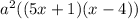Part B:
For this case we have the following polynomial:

`x^2 + 14x + 49`
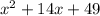
We factor the expression.
To do this, we write two numbers that added are 14 and multiplied are 49.
We have then:

`(x + 7) (x + 7)`
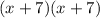Answer:

`(x + 7) (x + 7)`

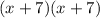Part C:
For this case we have the following polynomial:

`x ^ 2 -100`
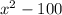
We observe that we have a binomial, therefore, we must factor.
To do this, we write two numbers that added are 0 and multiplied are -100.
We have then:

`(x + 10) (x-10)`
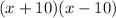Answer:

`(x + 10) (x-10)`