There are 106 different ways Saga can put 2 toppings on her ice cream, including the choice of no toppings. So Saga has 105 different ways of choosing the 2 toppings.
Let the total number of toppings be x. Saga has to choose 2 toppings, so this is a problem of combinations. Combination of 2 objects from can be written as nC2. There are total 105 ways to choosing the toppings, so we can write:
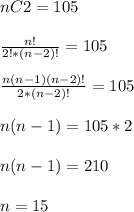
Solving the quadratic equation above we get n=15.
This means 15 different toppings were there at the ice cream store.