Question

Solve cos (x) tan (x) -1/2=0 over the interval [0,2π].

Answer 1

First, we are going to add
`(1)/(2)` from both sides of the equation:

`cos(x)tan(x)- (1)/(2) + (1)/(2) = (1)/(2)`

`cos(x)tan(x)= (1)/(2)`

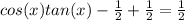
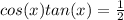
Next, we are going to use the trig identity:
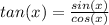
`tan(x)= (sin(x))/(cos(x))` to rewrite our expression:

`cos(x)tan(x)= (1)/(2)`

`cos(x) (sin(x))/(cos(x)) = (1)/(2)`

`sin(x)= (1)/(2)`

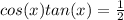
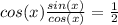
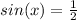
Finally, using our unitary circle, we can infer that
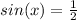
`sin(x)= (1)/(2)` from 0 to
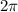
`2 \pi` when
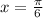
`x= ( \pi )/(6)` and
`x= (5 \pi )/(6)`

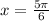
We can conclude that the solutions of the equation cos (x) tan (x) -1/2=0 over the interval [0,2π] are:
`x=( \pi )/(6),(5 \pi )/(6)`