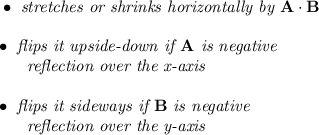

with that template in mind.
since the original or "parent" function is y = x²−4x+3, if we change the "x" argument to "x-2", we end up with a horizontal shift.
the x-2 part would be in the template the Bx+C part, with B = 1 and C = -2, or a horizontal shift to the right of 2/1 or 2 units.
since the parent function has a point at (2, -1), if we move that horizontally only to the right, we'd end up at (4, -1).