Question

What is the simplified base for the function f(x) = 2(27 cube rooted to the power of 2x

Answer 1

Remember:
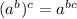`(a^b)^c=a^(bc)` and
`\sqrt[n]{a^b}=a^(b)/(n)`

Not sure if you mean

AAA.
`f(x)=2(\sqrt[3]{27})^(2x)`

or

BBB.
`2(\sqrt[3]{27^(2x)})`

Or

CCC.
`(2\sqrt[3]{27})^(2x)`

If AAA, go to AAAAAA

If BBB, go to BBBBB

If CCC, go to CCCCC

AAAAAAAAA

`f(x)=2(\sqrt[3]{27})^(2x)`

Simplify inside parenthaees first

`f(x)=2(\sqrt[3]{3^3})^(2x)`

`f(x)=2(3)^(2x)`

`f(x)=2((3)^2)^x`

`f(x)=2(9)^x`

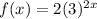
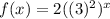
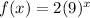
The base is 9

BBBBBBBB

`f(x)=2(\sqrt[3}{3^(6x)})`

`f(x)=2(3^(6x)/(3))`

`f(x)=2(3^(2x))`

`f(x)=2(3^2)^x`

`f(x)=2(9)^x`

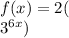
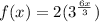
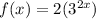
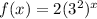
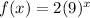
The base is 9

CCCCCCC

`f(x)=(2\sqrt[3]{27})^(2x)`

`f(x)=(2\sqrt[3]{3^3})^(2x)`

`f(x)=(2*3)^(2x)`

`f(x)=6^(2x)`

`f(x)=(6^2)^x`

`f(x)=36^x`

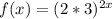
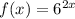
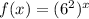
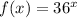
Base is 36

If it’s
`f(x)=2(\sqrt[3]{27})^(2x)` or
`f(x)=2(\sqrt[3]{27^(2x)})`, the base is 9

If it’s
`f(x)=(2\sqrt[3]{27})^(2x)`, the base is 36