Question

One jet flies at a ground speed of 75 miles per hour faster than another jet. on a particular flight the faster jet requires 3 hours and the slower one 3 hours and 36 minutes. what is the length of the flight

Answer 1

It is a distance-speed-time problem. Applying the general formula of
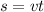
`s=vt`, we'll solve this problem. If the speed of the second jet is
`v`, then the speed of the first jet is
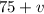
`75+v` according to the problem. The first jet requires 3 hours and 36 minutes (3.6 hours) and the second one 3 hours.
By setting up an equation we can write that
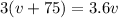
`3(v+75) = 3.6v` and
`v=375`
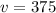
The length of flight is
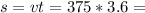
`s=vt=375*3.6=` or
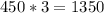
`450*3=1350` miles