Question

A satellite in a nearly circular orbit is 2000 km above earth's surface. the radius of earth is approximately 6400 km. if the satellite completes its orbit in 12 hours, calculate the speed of the satellite in kilometers per hour.

Answer 1

Velocity is computed using the formula:


`v= (d)/(t)`
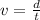
Where:
V = speed
d = distance traveled
t = time/period

First you need to consider that the orbit is circular. To get the measurement or the distance going around Earth, you will need to get the circumference of the path.


`C = 2 \pi r`

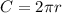
Where:
C = circumference
π = 3.14
r = radius


The Earth has a radius of 6,400km, but you also need to consider that the satellite is orbiting above the surface of the Earth, so you add in the 2,000km to that radius.

r = 6,400Km + 2,000Km = 8,400Km

Next step is to insert that into our circumference formula:


`C = 2 \pi r`

`C = 2 \pi 8,400Km`

`C = 52,778.76 Km`

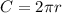
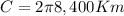
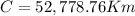
The distance traveled would then be 52,778.76Km

Now that we have the distance, we can then get the velocity:


`v= (d)/(t)`

`v= (52,778.76Km)/(12hrs)`

`v= 4,398.23km/hr`

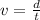
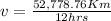
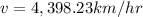
The speed of the satellite is 4,398.23km/hr.