Question

An observer is moving in space toward a distant star at 200 km/s while the star is moving toward the observer at 400 km/s; the relative velocity being 600 km/s of approach. what relative change in frequency of the light from the star as seen by the observer? (the speed of light in space is 3.00 ´ 105 km/s).

Answer 1

The correct answer is: 0.2% (decrease)

Step-by-step explanation:

The observed frequency can be found by using the following equation:

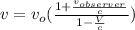
`v = v_o ( (1 + (v_(observer))/(c))/(1- (V)/(c)) )` --- (1)

Where
`v_(observer)` = Speed of the observer = 200 *1000 m/s
V = speed of the star = 400 *1000 m/s

Plug in the values in (1):
(1) =>
`v = v_o ( (1 + (200*10^3)/(3*10^8))/(1- (400*10^3)/(3*10^8)) )`


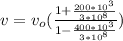
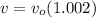
`v = v_o ( 1.002 )` --- (2)

Change in frequency is given as:
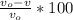
`(v_o - v)/(v_o) * 100`% --- (3)

Put (2) in (3):

`(v_o - 1.002*v_o)/(v_o) * 100`%

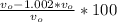
=> -0.2%

Negative sign shows that it decreases!

Hence it is 0.2% (decrease).