1 Answer

Ask a Question

Chase McCoy · Answer 1 · 2019-01-12T14:01:16+0000

This is a problem on a binomial probability distribution. A binomial probability distribution has fixed number of trials, n. In this case, n is equal to 316. Also, the trials in a binomial probability distribution must be independent. Each trial must have all outcomes classified into two categories--carnation or not carnation. Lastly, the probability of success remains the same in all trials.

The binomial probability formula is given by

$p\left(x\right)=C\left(n,\:x\right)p^x\left(q\right)^(n-x)$
where
n=number of trials
x=number of successes among n trials
p=probability of success in any one trial
q=probability of failure in any one trial (q=1-p)

So, from the given problem, the following quantities are given:

n=316

,

Part A
The probability of obtaining fewer than 40 (0 to 39) carnations is the summation of all the binomial probabilities from 0 to 39. That is

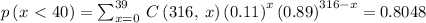
$p\left(x\ \textless \ 40\right)=\sum _(x=0)^(39)\:C\left(316,\:x\right)\left(0.11\right)^x\left(0.89\right)^(316-x)=0.8048$

Part B
The probability that at least 25 are carnations is the sum of binomial probabilities of x from 25 to 316. That is

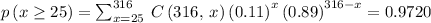$p\left(x\ge 25\right)=\sum _(x=25)^(316)\:C\left(316,\:x\right)\left(0.11\right)^x\left(0.89\right)^(316-x)=0.9720$

Part C
The probability that carnations are between 25 and 40 is given by the sum of individual binomial probabilities from 26 and 39. That is

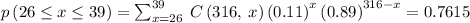
$p\left(26\le x\le 39\right)=\sum _(x=26)^(39)\:C\left(316,\:x\right)\left(0.11\right)^x\left(0.89\right)^(316-x)=0.7615$

Therefore, the probability that there are fewer than 40 carnations is 0.8048, at least 25 carnations is 0.9720, and between 25 and 40 is 0.7615.

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions