Question

wo systems of equations are shown below. The first equation in System B is the original equation in system A. The second equation in System B is the sum of that equation and a multiple of the second equation in System A. A. x + 3y = 11 → x + 3y = 11 5x − y = 17 → 15x − 3y = 51 15x = 62 B. x + 3y = 11 15x = 62 What is the solution to both systems A and B?

Answer 1

x=3.875, y=2.375

Explanation:

The system we are given is:

`\left \{ {{x+3y=11} \atop {5x-y=17}} \right.`

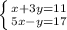
We will use elimination to solve this. We will make the coefficients of y the same by multiplying the bottom equation by 3:

`\left \{ {{x+3y=11} \atop {3(5x-y=17)}} \right. \\\\\left \{ {{x+3y=11} \atop {15x-3y=51}} \right.`

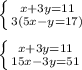
Since the coefficients of y are the same with different signs, we will add the equations to eliminate y:

`\left \{ {{x+3y=11} \atop {+(15x-3y=51)}} \right. \\\\16x=62`

Divide both sides by 16:

16x/16 = 62/16

x = 3.875

Now we substitute this in place of x:

3.875+3y = 11

Subtract 3.875 from each side:

3.875+3y-3.875 = 11-3.875

3y = 7.125

Divide both sides by 3:

3y/3 = 7.125/3

y = 2.375

Answer 2

A.)
x + 3y = 11
5x - y = 17 ⇒ 15x - 3y = 51
15x = 62

B.) x + 3y = 11
15x = 62

x + 3y = 11
5x - y = 17

x = 11 - 3y
5x - y = 17
5(11-3y) - y = 17
55 - 15y - y = 17
-16y = 17 - 55
-16y = -38
y = -38/-16
y = 2.375

x = 11 - 3y
x = 11 - 3(2.375)
x = 11 - 7.125
x = 3.875

x = 3.875 ; y = 2.375

x + 3y = 11
3.875 + 3(2.375) = 11
3.875 + 7.125 = 11
11 = 11