Question

The position of an object at a time t is given by s(t)=-4-2t. Find the instantaneous velocity at t=6 by finding the derivative

Answer 1

`\bf s(t)=4-2t\implies \cfrac{ds}{dt}=0-2\implies \left. \stackrel{v(t)}{\cfrac{ds}{dt}=-2} \right|_(t=6)\implies -2`

Answer 2

Velocity, s'(t)=-2

Explanation:

It is given that,

The position of an object at time t is given by following equation :

`s(t)=-4-2t`

We need to find the instantaneous velocity. We know that velocity is given by :

`v=(ds(t))/(dt)`

or

`s'(t)=-2`

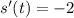
So, the instantaneous velocity at t = 6 seconds is -2 m/s i.e. s(6) = -2 Hence, this is the required solution.