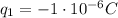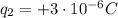Question

Two identical conducting spheres, having charges of opposite sign, attract each otherwith a force of 0.108 n when separated by 50.0 cm. the spheres are suddenly con-nected by a thin conducting wire, which is then removed, and thereafter the spheresrepel each other with a force of 0.0360 n. what were the initial charges on the spheres?

Answer 1

Let's start from the final situation. After the two spheres are connected with the conducting wire, the total charge distributes equally between the two spheres (because they are identical). We can call the charge on each sphere
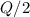
`Q/2`, with Q being the total charge.
The electrostatic force in this situation is 0.0360 N, so we can write

`F=k (( (Q)/(2) )^2)/(r^2)`
where k is the Coulomb's constant and
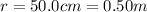
`r=50.0 cm=0.50 m` is the separation between the two spheres. Using F=0.0360 N, we can find the value of Q, the total charge shared between the two spheres:

`Q= \sqrt{ (4Fr^2)/(k) } = \sqrt{ (4(0.0360 N)(0.50 m)^2)/(8.99 \cdot 10^9 Nm^2C^(-2)) }=2.0 \cdot 10^(-6)C`

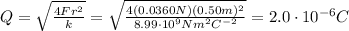
Now let's go back to the initial situation, before the conducting wire was attached; in this situation, the two spheres have a charge of
`q_1` and
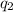
`q_2`, whose sum is Q:

`Q=q_1 + q_2`
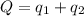
The electrostatic force between the two spheres in the initial situation is:

`F=k (q_1 q_2)/(r^2)`
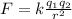
And since we know F=0.108 N, we find

`q_1 q_2 = (Fr^2)/(k) = ((0.108 N)(0.50 m)^2)/(8.99 \cdot 10^9 N m^2 C^(-2))=3.0 \cdot 10^(-12) C`
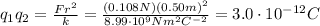
But the problem tells us that the two spheres have charges of opposite sign, so we must put a negative sign:

`-3.0 \cdot 10^(-12) C = q_1 q_2`

So now we have basically a system of 2 equations:

`2.0 \cdot 10^(-6) C = Q = q_1 + q_2`

`-3.0 \cdot 10^(-12) C = q_1 q_2`
If we solve it, we find the initial charge on the two spheres:

`q_1 = -1 \cdot 10^(-6)C`

`q_2 = +3 \cdot 10^(-6 ) C`