We have this parallelogram shown in the picture (just ignore the letters). Let's DK (in the picture it is AC) with x and CD (in the picture it is AD) with x-7. Applying Pythagoras theorem, we can write that DA (in the problem, in the picture it is AE) is
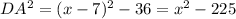
. Solving this equation, we find the value of x and it is 106/7. That's the value of DK. And CD=106/7-7=57/7