The first step for solving this expression is to multiply the parenthesis.
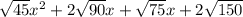
Simplify the first radical.
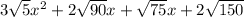
Simplify the second radical.
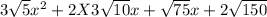
Simplify the third radical.
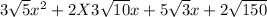
Simplify the final radical.
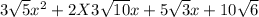
Lastly,, calculate the product of 2 × 3
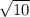
x to get your final answer.
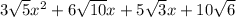
Let me know if you have any further questions.
:)