Question

How many 2-digit numbers are multiples of neither 5 nor 7?

Answer 1

Explanation:

You take the amount of 2-digit numbers there are (90) and subtract it from the amount of two digit numbers that are multiples of 5 and 7 (29). You should get 61.

Answer 2

Answer: The number 2-digit numbers are multiples of neither 5 nor 7 is 61.

Step-by-step explanation: We are given to find the number of 2-digit numbers that are multiples of neither 5 nor 7.

Let A denote the set of 2-digit numbers that are multiples of 5 and B denote the set of 2-digit numbers that are multiples of 7.

Then,

A = {10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95}

and

B = {14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98}

That is, n(A) = 18 and n(B) = 13.

Now, the set of 2-digit numbers that are multiples of both 5 and 7 is given by

`A\cap B=\{35, 70\}~~~~~~\Rightarrow n(A\cap B)=2.`

Therefore, the number of 2-digit numbers that are multiples of either 5 or 7 is given by

`n(A\cup B)=n(A)+n(B)-n(A\cup B)=18+13-2=29.`

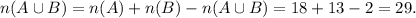
Now, there are 90 2 -digit numbers.

Thus, the number 2-digit numbers are multiples of neither 5 nor 7 is

90 - 29 = 61.

Hence, the total number of numbers is 61.