Question

Express the complex number in trigonometric form. -2 + 2square root of three i

Answer 1

4cos(120) + 4isin(120)

Answer 2

The required trigonometric form is
`4(\cos(60)-i\sin(60))`

Explanation:

Given : Complex number
`-2+2√(3)i`

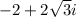
To find : Express the complex number in trigonometric form?

Solution :

The complex number
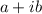`a+ib` trigonometric form is
`r(\cos\theta+i\sin\theta)`

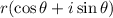
Where,
`r=√(a^2+b^2)`

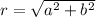
and
`\theta=\tan^(-1)((b)/(a))`

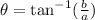
On comparing with given complex number
`-2+2√(3)i`

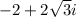
a=-2 and
`b=2√(3)`

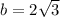
Substitute the value,

`r=√(a^2+b^2)`

`r=\sqrt{(-2)^2+(2√(3))^2}`

`r=√(4+12)`

`r=√(16)`

`r=4`

`\theta=\tan^(-1)((b)/(a))`

`\theta=\tan^(-1)((2\sqrt3)/(-2))`

`\theta=\tan^(-1)(-sqrt3)`

`\theta=\tan^(-1)(\tan(-60))`

`\theta=-60`

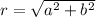
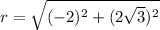
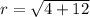
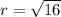
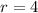
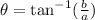
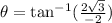
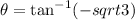
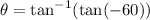
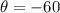
Substituting all values in the formula,

`r(\cos\theta+i\sin\theta)`

`4(\cos(-60)+i\sin(-60))`

`4(\cos(60)-i\sin(60))`

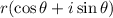
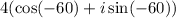
Therefore, The required trigonometric form is
`4(\cos(60)-i\sin(60))`