The electric field produced by a single point charge is given by:
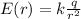
where
k is the Coulomb's constant
q is the charge
r is the distance from the charge
In our problem, the charge is
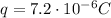
, while the distance is

, therefore the intensity of the electric field at that distance is
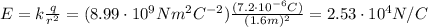
and since the charge is positive, the electric field is directed away from the charge (so, eastwards)