Question

A production process produces 2% defective parts. a sample of 5 parts from the production is selected. what is the probability that the sample contains exactly two defective parts? use the binomial probability function and show your computations to answer this question.

Answer 1

Possible outcomes: defective/non defective

Applying Binomial distribution equation
p(x) = [N!/x!(N-x)!]*(p^x)(q)^N-x

Where,
p = 2% = 0.02
N = 5
And then,
q = 1-p = 1-0.02 = 0.98
x = 2
N-x = 5-2 = 3

Substituting;
p(2) = [5!/2!(5-2)!]*0.02^2*0.98^3 = 0.00376 = 0.376%

Answer 2

Probability of a sample that contains exactly two defective parts is .0037 or .37%

Explanation:

As we know if P is the probability of achieving k results in n trials then probability formula is P =
`\binom{n}{k}p^(K)q^(n-k)`

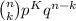
In this formula n = number of trials

k = number of success

(n-k) = number of failures

p = probability of success in one trial

q = (1-p) = probability of failure in one trial

In this sum n = 5

k = 2

number failures (n-k) = (5-2) = 3

p = 2% which can be written as .02

q = 98% Which can be written as .98

Now putting these values in the formula

P =
`\binom{5}{2}(.02)^(2)(.98)^(5-2)`

P =
`\binom{5}{2}(.02)^(2)(.98)^(3)`

`\binom{5}{2}= 5!/3!2!`

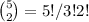
= 5×4×3×2×1/3×2×1×2×1

= 5×2 =10

P = 10×(.02)²×(.98)³

= .0037 or .37%