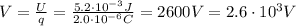1) The electric potential energy is equal to the product between the electric potential and the charge:
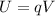
where
q is the charge
V is the electric potential
In our problem, the charge on the rod is
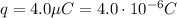
, while its potential energy is
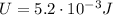
, therefore we can re-arrange the previous formula to get the electric potential at the tip:
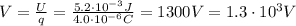
2) By using the same formula, If the charge is changed to
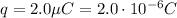
, the electric potential will be: