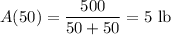Let
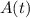
be the amount of salt (in pounds) in the tank at time

. We're given that
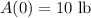
.
The rate at which the amount of salt in the tank changes is given by the ODE
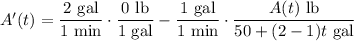
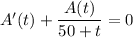
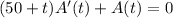
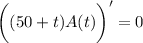
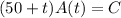
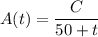
Given that
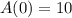
, we find that
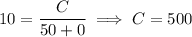
so that the amount of salt in the tank is described by

The tank will be filled when
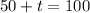
, or after

minutes. At this time, the amount of salt in the tank is