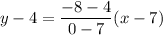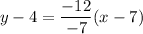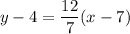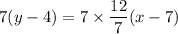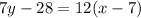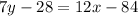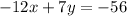Question

Write the equation of the line that passes through the given points:

(7, 4) and (0, -8)

​

Answer 1

`12x - 7y = 56`

Explanation:

Equation of the line that passes through points (x1, y1) and (x2, y2):

`y - y_1 = (y_2 - y_1)/(x_2 - x_1)(x - x_1)`

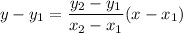
Choose one point to be point 1 with coordinates x1 and y1, and the other point will be point 2 with coordinates x2 and y2.

Let point (7, 4) be point 1. Then, x1 = 7, and y1 = 4.

Then, point 2 is (0, -8) with x2 = 0, and y2 = -8.

Now plug in the values of the coordinates into the equation above.

`y - 4 = (-8 - 4)/(0 - 7)(x - 7)`

`y - 4 = (-12)/(-7)(x - 7)`

`y - 4 = (12)/(7)(x - 7)`

`7(y - 4) = 7 * (12)/(7)(x - 7)`

`7y - 28 = 12(x - 7)`

`7y - 28 = 12x - 84`

`-12x + 7y = -56`

`12x - 7y = 56`

Answer 2

Explanation:

first we find the slope(m)

m = (y2 - y1) / (x2 - x1)

(7,4)...x1 = 7 and y1 = 4

(0,-8)..x2 = 0 and y2 = -8

sub

m = (-8 - 4) / (0 - 7)

m = -12/-7

m = 12/7

now we use y = mx + b

slope(m) = 12/7

use either of ur points....(7,4)....x = 7 and y = 4....so we know x, y and the slope(m)....now we need to find b, the y int

so we sub

4 = 12/7(7) + b

4 = 12 + b

4 - 12 = b

-8 = b

so ur equation is : y = 12/7x - 8 <===