Question

One focus of a hyperbola is located at (−1, 7). One vertex of the hyperbola is located at (−1, 5). The center is (−1, −3).

What is the equation of the hyperbola?

A. (y + 1)²/64 - (x + 3)²/36 = 1

B. (y - 1)²/64 - (x - 3)²/36 = 1

C. (y + 3)²/64 - (x + 1)²/36 = 1

D. (y - 3)²/64 - (x - 1)²/36 = 1

Answer 1

C. (y + 3)²/64 - (x + 1)²/36 = 1

Explanation:

This is a hyperbola with a vertically tranversed axis, so the general equation for it is:

`((y-k)^(2) )/(a^(2))-((x-h)^(2) )/(b^(2))=1`

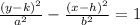
where h and k are the coordinate for the center (h, k)

we're given center is (−1, −3), so

h = -1

k = -3

`((y-(-3))^(2) )/(a^(2))-((x-(-1))^(2) )/(b^(2))=1`

`((y+3)^(2) )/(a^(2))-((x+1)^(2) )/(b^(2))=1`

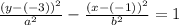
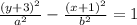
The information about "One focus of a hyperbola is located at (−1, 7). One vertex of the hyperbola is located at (−1, 5)" are irrelevant because the a and b values are the same for all the answers. So we literally only needed the center of the hyperbola to find our answer.

The only answer with (y+3) and (x+1) is C.